What is a "TeX token"?
The motivation, and methodology used, to produce a series of articles on TeX tokens and related concepts is discussed in this article A New Series of Articles: TeX Tokens and Related Concepts—But Why (and How)? As noted in that article, throughout this series we are basing our discussions and explanations on insights gained through a custom build of Knuth’s original TeX program—using it to produce a series of articles that aims to provide simple descriptions and easy-to-follow explanations of key TeX concepts.
Introduction: what is our aim?
In this article we find out exactly what a TeX token is by tracing the processing journey from characters in the input file to the actual creation of TeX tokens. In practice, it is quite complex so we have reduced the process down to its core essentials, striving to make it easy to follow and understand whilst preserving technical accuracy.
We start by introducing some important internal TeX concepts: primitives, command codes and command modifiers. From there, we use a very simple macro example to see exactly how TeX processes the command \def and the resulting token that TeX creates to represent that command.
We conclude with a brief look at how TeX creates tokens to represent characters and how a character’s \catcode does indeed become permanently attached to a character token—something often mentioned in books about TeX but here we see exactly how that is achieved.
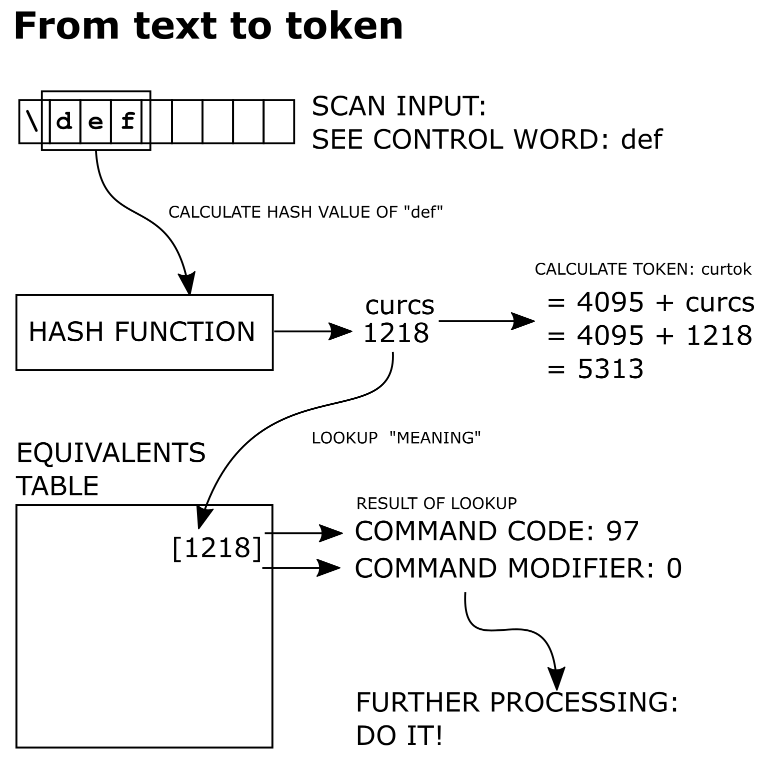
The following graphic shows the journey we will summarize—from input text to TeX tokens:
But first: primitives and command codes
Every TeX engine (Knuthian TeX, pdfTeX, XeTeX, LuaTeX) understands a number of built-in commands: the so-called primitives—the fundamental building-block commands that underpin TeX’s programmability. They are called “primitive” because, unlike user-defined macros, they are not constructed from other commands and cannot be further reduced to simpler instructions. For Knuth’s TeX there are approximately 320 primitives—although we should note that other TeX engines such as pdfTeX, XeTeX and LuaTeX have all added new commands to Knuth’s original program and will contain primitives that are not present in Knuth’s TeX software.
Internally, TeX assigns a numeric command code to all commands—whether they are user-defined macros or built-in primitives. These command codes are not accessible to the TeX user, they are simply part of the internal mechanics of TeX’s processing but it is useful to know about them for later discussion of TeX tokens.
Groups of commands that have related functionality share the same command code. For example, the \def, \gdef, \edef and \xdef primitives all are used to define macros and share the command code of 97 (in Knuth’s TeX). Clearly, those 4 macro-definition commands each create macros in a slightly different way; consequently, during processing, TeX needs a way to distinguish between them.
A command code on its own (such as 97) cannot tell you which macro-creation command is under consideration; so, as you might expect, each TeX command is assigned an additional piece of information called its command modifier (see examples below).
Command modifiers: two types
Command modifiers fall into two categories which we’ll refer to as “Type 1” and “Type 2”—TeX does not use this terminology, it’s just convenient to do so here:
- Type 1: Simple integer values that TeX can, if required, use to distinguish between commands sharing the same command code.
- Type 2: An integer value that is a numeric location in TeX’s memory telling TeX where it needs to go to lookup information for that command. For example, this applies to user-defined commands (macros) where the command modifier tells TeX where the macro definition is stored in memory.
Type 1 command modifiers (an example)
As noted, in Knuth’s TeX the four primitive commands for defining macros: \def, \gdef, \edef, \xdef all share the command code of 97: they are differentiated through their command modifiers, which are listed in the following table:
| Command | Command code |
Command modifier |
|---|---|---|
\def
|
97 | 0 |
\gdef
|
97 | 1 |
\edef
|
97 | 2 |
\xdef
|
97 | 3 |
By way of a second example, Knuth decided to implement the commands \openout, \write, \closeout, \special, \immediate and \setlanguage as “extensions” to TeX, purely to show how you can add new primitives to TeX. In this case, those commands don’t really share “similar functionality” except that Knuth decided to group them together for purposes of explaining how to extend TeX. Those 6 commands are classified as “extensions” and grouped together with the command code value of 59 but each one has an appropriate command modifier to differentiate it from the others:
| Command | Command code |
Command modifier |
|---|---|---|
\openout
|
59 | 0 |
\write
|
59 | 1 |
\closeout
|
59 | 2 |
\special
|
59 | 3 |
\immediate
|
59 | 4 |
\setlanguage
|
59 | 5 |
Type 2 command modifiers (a brief explanation)
Although all command modifiers are integers, Type 2 modifiers need a little more explanation. These command modifiers are referred to in TeX as “pointers” because they point to a location in memory where TeX can find additional information for that command. This may sound a little vague but the way TeX uses these pointers to lookup information is quite varied and a fuller explanation would distract from the core aim of this article. One example may help: macros. When a macro command is defined TeX will need to store the replacement text somewhere in memory. As we’ll see below, user-defined macros have command codes between 111 and 114 with a command modifier that is a pointer into memory telling TeX where its replacement text (the macro definition) is stored.
Command codes: expandable and non-expandable
In Knuth’s source code to TeX the command codes vary from 0 to 120—note that some codes within that range are purely for specialist internal use and are not assigned to commands which are accessible to the user. It’s worth noting that other TeX engines such as pdfTeX, XeTeX and LuaTeX have all added new commands to Knuth’s original set and will contain more primitives, and corresponding command codes; however, the principles outlined here are core to all TeX-based engines derived from Knuth’s source code.
The collection of command codes is split into two main sets:
- non-expandable commands: have command codes less than or equal to 100;
- expandable commands: have command codes greater than 100, up to a maximum value of 120. The range 101 to 120 includes user-defined macros plus commands such as
\csname,\expandafterand\the.
Non-expandable commands typically carry out assignment of a value to an internal parameter or directly produce material that can be typeset. Expandable commands typically “inject” a stream of tokens into TeX’s current processing activity or modify the order of token processing.
As noted above, all macros (user-defined commands) are given command codes between 111 and 114: the different values reflect whether the macro was defined as \long, \outer, both or neither. Here is an example:
| Macro type | Example | Comment |
|---|---|---|
| Non-long, non-outer | \def\ohyeah{....}
|
\ohyeah command code=111
|
| Long, non-outer | \long\def\ohyeah{....}
|
\ohyeah command code=112
|
| Non-long, outer | \outer\def\ohyeah{....}
|
\ohyeah command code=113
|
| Long outer | \long\outer\def\ohyeah{....}
|
\ohyeah command code=114
|
As a reminder on command modifiers, when a macro is defined TeX will store the macro’s definition in some location in memory: that location (a pointer) will become the command modifier for the macro command which will be stored with a command of 111 to 114 depending on how it was defined. The actual name assigned to a user-defined macro does not really matter: after processing of the input they’ll all be assigned a command code varying from 111–114 and, ultimately, all commands that TeX reads from your input, whether they are primitives or user-defined macros, are eventually converted into a numeric representation called a token.
The journey from input text to TeX tokens
In this section we’ll use a very simple macro example to see exactly how TeX processes the command \def to create a token which represents the \def command. The detailed processing activity of TeX can be extremely complex so we are not using macro parameters or delimiters because that would add complexity and distract from our journey.
Suppose that your TeX input file contains the following line:
\def\ohyeah{Overleaf is cool!}
As TeX begins to process this line of input it checks the \catcode of each character and sees the first character is \ (first character of \def). It detects (looks it up in an internal table) that \ has \catcode 0 which means it introduces the start of a control sequence. Of course, you can redefine any character to have \catcode 0 but we’ll assume that conventional definitions of plain TeX or LaTeX are being used.
Strictly speaking, the term control sequence has two sub-categories: control word and control symbol:
- control word: a sequence of characters with
\catcodeletter (11); - control symbol: a single character whose
\catcodeis not letter (11).
At this point, the \ character has done its job and is now finished with. On detecting an escape character, TeX’s response is to start reading all subsequent characters in the input with a view to detecting a control word or a control symbol.
After the initial \, TeX immediately detects the d: a character whose \catcode is 11 which tells TeX that it has found the first letter of a control word. It continues scanning subsequent characters until it finally detects a character that does not have \catcode letter (11). All subsequent characters (after the initial \) with \catcode 11 (letter) are considered to form the name of a control word: i.e., the name of a command—maybe a macro or a primitive but TeX, as yet, has no idea which type of command it is. At this point is is simply a string of characters.
So, in our example TeX happily scans along, checking each character, until it reaches the initial \ of \ohyeah which also has \catcode 0. TeX recognizes that it has scanned too far and politely returns that \ back into the text stream so that it becomes the next character to be seen during further scanning of the text.
At this point, TeX has identified a string (def) which it knows form the text of a control word comprising three characters, each with \catcode 11 (d, e and f). What TeX now needs to do is find out what def means: what does it to do? As you may have guessed, TeX needs to find the command code and command identifier for def so that it can work out what to do with this command.
Making a hash of it
Having detected a control word (def), the first thing that TeX does is to “convert” the string of characters (def in our example) into an integer number by using something called a hashing function. We don’t need to be too concerned with the details, an outline will suffice. In essence, TeX looks at every character in the control word it has just detected and uses the ASCII code value (or Unicode value for XeTeX/LuaTeX) of each character to calculate a number called a hash value: it is just a simple integer.
As part of this hash calculation process TeX will also check to see if the string of characters in the newly-detected control word is already known to it.
The human-readable text of all commands, whether they are primitives or user-defined macros, are stored away within an internal storage area called the string pool. TeX has to do this because it might need to output the human-readable name of a command—for example, when TeX needs to report an error and provide the name of the offending command. For example, our macro \def\ohyeah{Overleaf is cool!} is defining a new command called \ohyeah and TeX will (at a later stage) not only need to calculate a hash value for ohyeah (without the initial \ character) but also store the text string (human readable) form in case it needs to use it for error reporting (or other tasks).
If you want more detail about TeX’s string handling processes I have written about this on my personal blog site.
The end result is that the string of characters representing the command def is turned into the numeric value of 1218 (that is the actual value calculated by TeX). At this point the individual characters d, e and f are no longer part of the main story—they’ve been read from the input and have done their job: from now on it’s all about integers and tokens—we will soon see what a token actually is! Internally, TeX refers to these hash value numbers as the current control sequence but in the source code that term is shortened to a variable called curcs. TeX’s source code is full of very short, often rather cryptic, variable names.
But what does TeX actually do with this freshly-minted integer value of 1218? How does TeX find out that the original string def, now represented by the integer 1218, actually refers to an instruction to define a macro? The answer is that TeX has a sort of internal “filing cabinet” where it stores the current meaning and value of every command it curently knows about—whether that command is a user-defined macro or a built-in primitive. The reason TeX went to the trouble of converting def into the hash value of 1218 (now stored in the variable called curcs) is to use it for looking-up the meaning of def. TeX will, of course, repeat this hash calculation exercise for all control words it detects in the input—though, of course, different control words yield different integer values from the hashing function: that’s the whole idea.
TeX’s internal “filing cabinet” is called the equivalents table and is the topic of the next section.
Consulting the equivalents table
Just to recap, let’s see what we’ve learned so far:
\introduces the start of a control sequence (either a control symbol or a control word).- If the first character after the
\has\catcode11 (letter) then it is the start of a control word. - For control words TeX scans to check for all subsequent input characters that have
\catcode11 and will stop scanning as soon as it finds the first character that does not have a\catcodeof 11. - The string of input characters (following the
\) which have\catcode11 are considered to be a control word that the user has typed: a command asking TeX to “do something”. - To begin the process of “doing something” TeX converts the string of characters in the control word into an integer. It does this using a so-called hashing function which outputs an integer.
- The integer (calculated hash value) is referred to as the current control sequence, but TeX gives it the shorter name of
curcs. - In our example, the control word
defis converted into the value 1218—which is stored in a variable calledcurcs: i.e.,curcs=1218.
TeX now needs to find out what the newly detected current control sequence actually means—what does TeX do with it?
A note on grouping: the need to save and restore information
Here, we will take a little detour to remind ourselves that TeX has the ability to save and restore information: i.e., it has some form of in-built “memory”.
Anyone who has written even the simplest macro should be aware of TeX’s grouping mechanism—for example, using \def to create macros within a group. Unless you apply the \global prefix to \def-created macros defined within a group, the value or meaning of that macro only persists within that group (and those below it): its definition is lost when the group is finished. For example, if you define a simple macro inside a group, like this:
{\def\foo{Hello}}
and try to use \foo outside the group
{\def\foo{Hello}}% \foo defined within a group (note: no use of \global)
\foo %<--- no longer defined, now undefined
then we get the beloved error: Undefined control sequence. \foo only has meaning inside the group (and its sub groups) in which it was defined. Furthermore, when you redefine a macro inside a group the new value can be lost when the group ends and the previous meaning (which existed outside the group) is restored.
\def\foo{Goodbye}
\foo\par% Outputs Goodbye
{\def\foo{Hello}% Redefined inside a group:
{Inside 2nd level group: \foo\par}}% Used inside 2nd level group: \foo outputs Hello
Outside group old value restored: \foo\par% Outputs Goodbye
The purpose of these simple examples is to point to TeX having some sort of “storage mechanism” or “memory” which saves/restores the “meaning” of commands—and, of course, it does. We hinted at this in the previous section: that “storage mechanism” or “filing cabinet” is a large internal table called the equivalents table. It is in there that TeX stores the current meaning or values of all the commands it currently knows about—the built-in primitives and user-defined macros.
The equivalents table: by analogy
To explain the equivalents table we’ll proceed by analogy. We’ll continue to use the notion of a filing cabinet with thousands of small drawers, each one labelled with a unique integer. At this stage in the processing TeX says, in effect:
“OK, I have this integer value of 1218 that I just calculated and saved in a variable called curcs. I now need to find out what it means: to do that I'll go and look in drawer number 1218 of my filing cabinet to see what it says in there.”
TeX uses 1218 to locate the correct drawer and there it finds a small note which contains three pieces of information whose names are those used in TeX’s source code:
eq_level:the level of grouping at which this entry was defined (level 1 = globally defined). We saw the effects of grouping in action above: here in the equivalents table is where that grouping level information is stored;eq_type:the command code for this entry;equiv:current “value” of this entry—it can be a simple integer such as the command modifier mentioned above, or a pointer to an area in memory; for example, the memory location for the collection of tokens representing a macro definition.
So, our hash value of 1218 (saved in the variable curcs) has, in effect, been used as the key to access a drawer that contains the current meaning and value of the command we originally typed in as the string of letters \def.
Within the source code of the TeX program, the eq_type for any command is stored using a variable called curcmd and the value of equiv is stored in a variable called curchr.
What does the equivalents table say for def?
As noted, the hash value calculated for any command is saved in a variable called curcs; hence for def we have curcs=1218. On looking at location 1218 in the equivalents table, TeX will find the following information:
curcmd=97. This is the command code for\def;curchr=0. This is the command modifier for\def.
\def is a primitive (built-in) TeX command and unless it has been redefined somewhere, the third and final piece of information should be eq_level=1 indicating that the meaning of \def is defined globally and not restricted to some lower level of grouping. Internally, the value of eq_level attached to a command plays an extremely important role within TeX’s grouping mechanism but we won’t consider this any further.
The following graphic summarizes the explanation we have worked through:

TeX tokens for commands
Having waded through the explanations above, the actual calculation of TeX tokens for control sequences turns out to be really very simple. TeX uses the value of curcs (1218) from the hash function to create a simple integer that it calls a token. The calculation to generate a token from the value of curcs is:
curtok = 4095 + curcs
TeX stores the value of the current token (most recently calculated) in a variable called curtok.
So, in conclusion, the TeX token representing the \def command is 4095 + 1218 = 5313.
And that’s it for TeX tokens which represent command sequences: they are simply an integer number that is calculated from a hash table value plus 4095.
TeX tokens for characters
When TeX needs to create a token representing a character it uses the following, equally simple, calculation:
curtok = 256*catcode + (ASCII value of character)
Note that slightly different calculations are used for Unicode-aware engines such as LuaTeX.
For example, the TeX token representing a space character with \catcode 10 and ASCII value 32 is:
256*10 + 32 = 2592
Token lists containing characters
When you create a simple token list with, for example,
\toks100={Hello}
TeX will create the following list of tokens and store them away in memory for later use:
- H→ 256 × 11 + 72 = 2888
- e→ 256 × 11 + 101 = 2917
- l→ 256 × 11 +108 = 2924
- l→ 256 × 11 +108 = 2924
- o→256 × 11 + 111 = 2927
Deep inside TeX’s memory the token register 100 will provide access to the storage location of “Hello”, saved as 5 token values: 2888, 2917, 2924, 2924, 2927. Note that these tokens combine each character’s ASCII code and the value of its \catcodeat point they are turned into tokens (tokenized). Once characters have been converted to character tokens, the \catcode value attached to them is permanent and is stored within the tokens for later use when the user says, for example, \the\toks100.
As noted, a character token is calculated from 256*catcode + (ASCII value) whereas a control sequence token is calculated from 4095 + curcs where curcs is the hash value of the control word (text string of a user-typed command) detected in the input by TeX. It is worth noting that character tokens are always less than 4095. Hence TeX can easily determine if a particular token represents a control sequence (a command) or a character and then work out which control sequence or character and \catcode pair is in encoded into that token.