LaTeX templates and examples — Math

A template and examples for upper level physics students taking quantum mechanics at St. Mary's College of Maryland. Includes examples of kets and column vectors.

mathbook in Arabic

Template for the class practice 6

Demonstração do teorema de Morley

Template for the class practice 5

template for the class practice 4

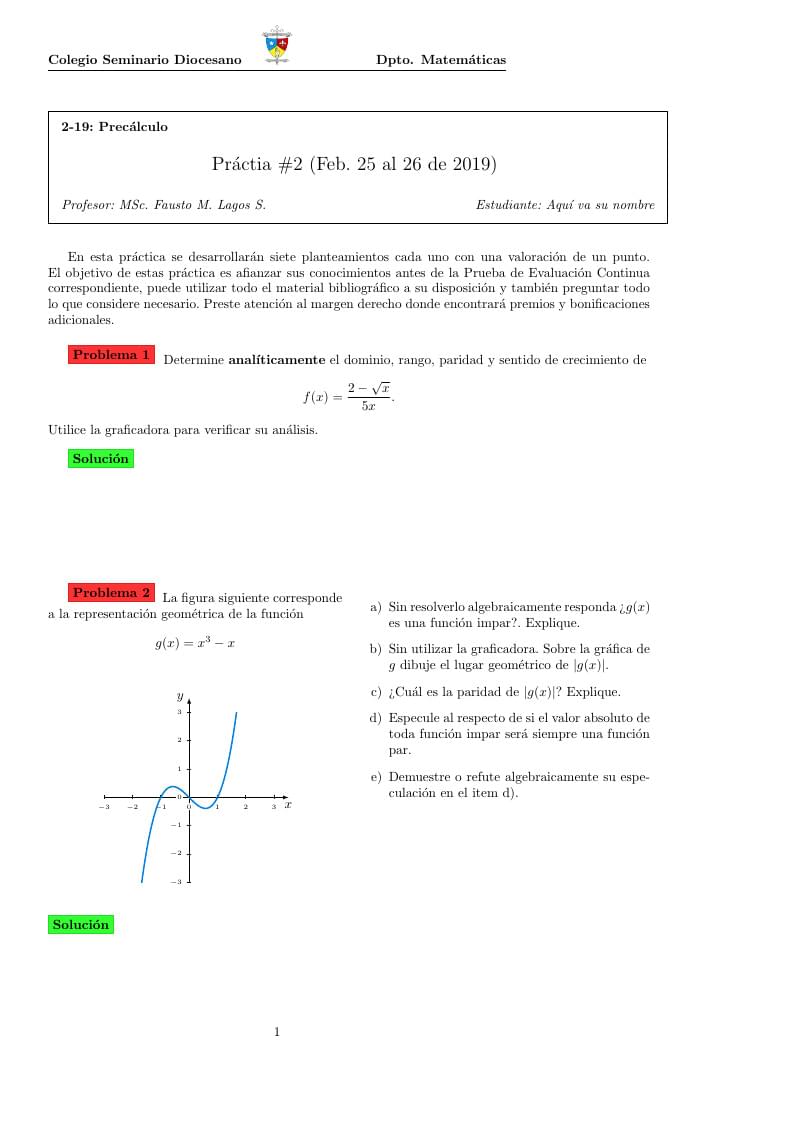
Template to resolve practice 2 in Calculus course 2-19

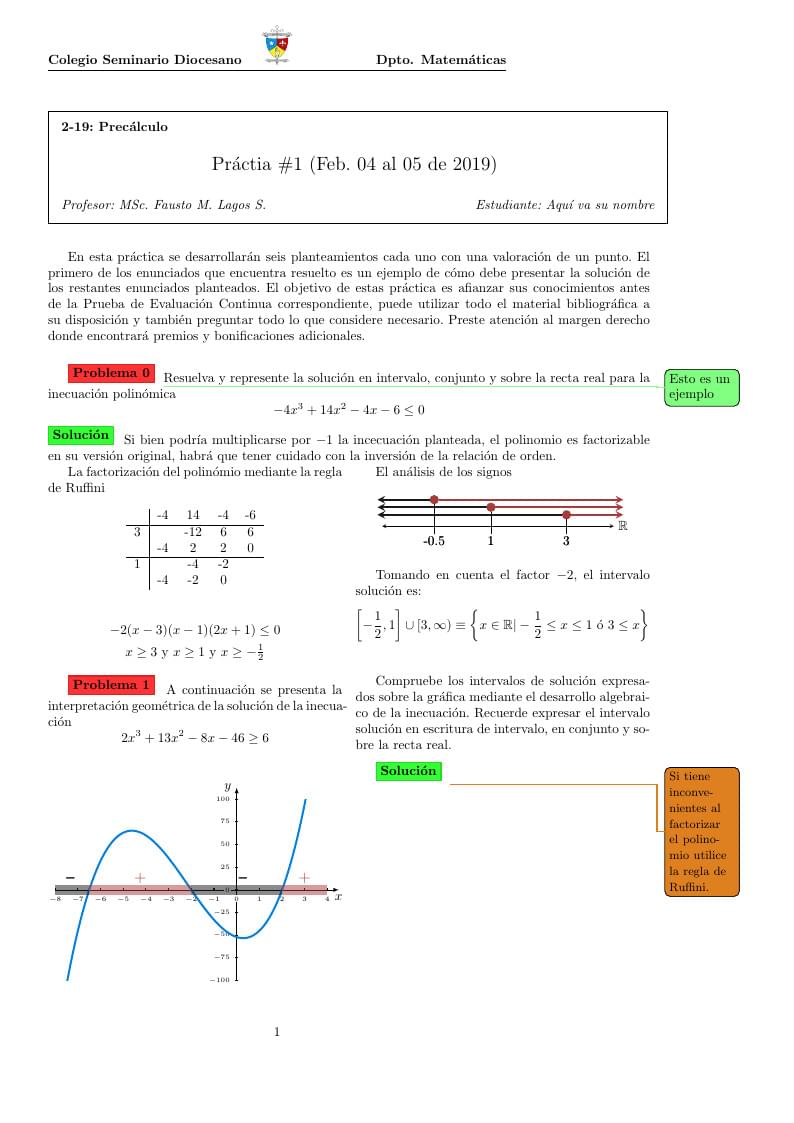
Template for the class practice 1.

This study is focused on lives of twelve women who prepared their doctorates in mathematics at the Faculty of Philosophy of the German University in Prague in the years 1882–1945, respectively at the Faculty of Science of the Czech University in Prague in the years 1882–1920 and 1921–1945 (known as Charles University in Prague in the latter period). In the first part, a short description of the historical background about women's studies at the universities in the Czech lands and a statistical overview of all PhD degrees in mathematics awarded at both universities in Prague is given for a better understanding of the situation with women's doctoral procedures. In the second part, a description of the successful doctoral procedures in mathematics of three women at the German University in Prague and of eight women at Charles University in Prague, as well as one unsuccessful doctoral procedure, are presented.